Fibonacci e la Sezione Aurea

“La matematica è l’alfabeto in cui Dio ha scritto l’Universo. La filosofia naturale è scritta in questo grandissimo libro che continuamente ci sta aperto innanzi agli occhi, io dico l’universo, ma non si può intendere se prima non s’impara a intender la lingua e conoscer i caratteri nei quali è scritto. Egli è scritto in lingua matematica, e i caratteri son triangoli, cerchi ed altre figure geometriche, senza i quali mezzi è impossibile a intenderne umanamente parola; senza questi è un aggirarsi vanamente per un oscuro labirinto.”

(Galileo Galilei)

In matematica, la successione di Fibonacci, è una successione di numeri interi positivi in cui ciascun numero è la somma dei due precedenti. Leonardo Pisano detto il Fibonacci (1175-1250), individuò questa serie per la prima volta nel 1202, per risolvere un problema pratico: quante coppie di conigli si ottengono in un anno da una sola coppia supponendo che produca ogni mese (tranne il primo) una nuova coppia che a sua volta diventa fertile a partire dal secondo mese? La risposta è 144 coppie di conigli. In questa serie ogni numero è il risultato della somma dei due precedenti: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34… fino all’infinito. Fino al XIX secolo a questa successione non fu attribuita alcuna importanza, finché si scoprì che può essere applicata, per esempio, nel calcolo delle probabilità, nella sezione aurea e nel triangolo aureo. I numeri di Fibonacci si trovano anche in natura, per esempio nella disposizione delle foglie.

In Botanica

In molti alberi, scegliendo una foglia su uno stelo e assegnandole il numero “0”, contando il numero di foglie fino ad arrivare a una perfettamente allineata con la foglia “0”, probabilmente si troverà un numero di Fibonacci. Anche i petali di moltissimi fiori sono un numero di Fibonacci.

Quasi tutti i fiori hanno tre o cinque o otto o tredici o ventuno o trentaquattro o cinquantacinque o ottantanove petali: ad esempio i gigli ne hanno tre, i ranuncoli cinque, il delphinium spesso ne ha otto, la calendula tredici, l’astro ventuno, e le margherite di solito ne hanno trentaquattro o cinquantacinque o ottantanove.

La Disposizione dei Fiori nel Capolino del Girasole

I numeri di Fibonacci sono presenti anche in altre piante come il girasole; difatti i piccoli fiori al centro del girasole (che è in effetti una infiorescenza) sono disposti lungo due insiemi di spirali che girano rispettivamente in senso orario e antiorario.

I pistilli sulle corolle dei fiori spesso si dispongono secondo uno schema preciso formato da spirali il cui numero corrisponde ad uno della serie di Fibonacci. Di solito le spirali orientate in senso orario sono trentaquattro mentre quelle orientate in senso antiorario cinquantacinque (due numeri di Fibonacci); altre volte sono rispettivamente cinquantacinque e ottantanove, o ottantanove e centoquarantaquattro. Si tratta sempre di numeri di Fibonacci consecutivi.

I numeri di Fibonacci sono presenti anche nel numero di infiorescenze di ortaggi come il Broccolo romanesco.
Le foglie sono disposte sui rami in modo tale da non coprirsi l’una con l’altra per permettere a ciascuna di esse di ricevere la luce del sole. Se prendiamo come punto di partenza la prima foglia di un ramo e contiamo quante foglie ci sono fino a quella perfettamente allineata spesso questo numero è un numero di Fibonacci e anche il numero di giri in senso orario o antiorario che si compiono per raggiungere tale foglia allineata dovrebbe essere un numero di Fibonacci. Il rapporto tra il numero di foglie e il numero di giri si chiama “rapporto fillotattico” (vedi Fillotassi).

Nel Corpo Umano

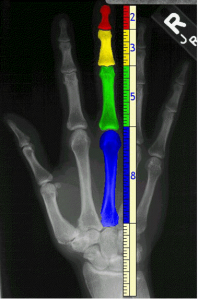
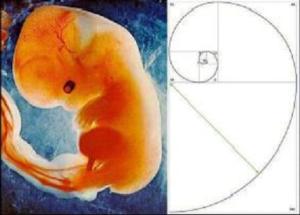
Il rapporto fra le lunghezze delle falangi del dito medio e anulare di un uomo adulto è aureo, come anche il rapporto tra la lunghezza del braccio e l’avambraccio, e tra la lunghezza della gamba e la sua parte inferiore.

In Geometria e in Natura

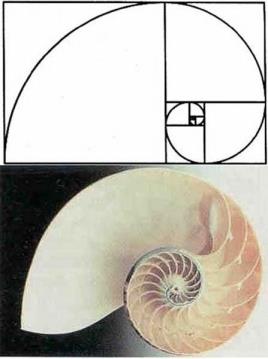
La spirale di Fibonacci, creata mediante l’unione di quadrati con i lati equivalenti ai numeri della successione di Fibonacci.

Se si disegna un rettangolo con i lati in rapporto aureo fra di loro, lo si può dividere in un quadrato e un altro rettangolo, simile a quello grande nel senso che anche i suoi lati stanno fra loro nel rapporto aureo. A questo punto il rettangolo minore può essere diviso in un quadrato e un rettangolo che ha pure i lati in rapporto aureo, e così via. La curva che passa per vertici consecutivi di questa successione di rettangoli è una spirale che troviamo spesso nelle conchiglie e nella disposizione dei semi del girasole sopra descritta e delle foglie su un ramo.

Sezione Aurea

La Sezione Aurea è il punto di divisione di un segmento in modo tale che il rapporto tra le due parti, la più piccola con la più grande, sia uguale al rapporto della parte più grande con tutto il segmento. Tale rapporto è un numero irrazionale le cui mirabili proprietà matematiche erano conosciute dall’antichità più estrema. Poiché indica uno sviluppo di crescita costante, espresso con una spirale che si sviluppa all’infinito, era considerato il sigillo del principio creativo, che si osserva riprodotto infinite volte in natura, dalla disposizione dei germogli e dei semi nelle piante ala spirale delle conchiglie dei molluschi alla conformazione dei cristalli, ed era venerato come espressione diretta del potere divino. La gran parte degli edifici sacri esibiscono in qualche modo nelle loro proporzioni la Sezione Aurea.

La proporzione aurea fu molto utilizzata dagli antichi Greci come rapporto armonico nelle costruzioni architettoniche, le ritroviamo nelle piramide egizie e nel Partenone nell’Acropoli Ateniese, e nelle rappresentazioni scultoree, per esempio nelle proporzioni delle Cariatidi che reggono l’Eretteo. Il rapporto aureo fu largamente ripreso anche nel Rinascimento: le dimensioni della Monnalisa, di Leonardo da Vinci, sono in rapporto aureo. E ancora fino ai giorni nostri, nell’architettura moderna: il Palazzo di Vetro delle Nazione Unite ha proporzioni auree. La sequenza di Fibonacci è abbondantemente rappresentata anche in musica, ad esempio nelle “fughe” di Johann Sebastian Bach, nelle sonate di Mozart, nella Quinta Sinfonia di Beethoven, nella Sonata in la D 959 di Schubert; l’esempio più elevato di applicazione su vasta scala degli stilemi improntati alla proporzione aurea è dato dalla Sagra della Primavera di Strawinski.